Today’s experiment is very simple but hopefully fascinating for even very young children. We’re going to investigate which solids dissolve in water.
When a substance dissolves in water, you can’t see it anymore; it’s still there but has mixed with the water to make a transparent liquid called a solution.
We call substances that dissolve in water soluble. Sugar and salt are examples of soluble substances.
Substances that do not dissolve in water are called insoluble. Sand and flour are examples of insoluble substances.

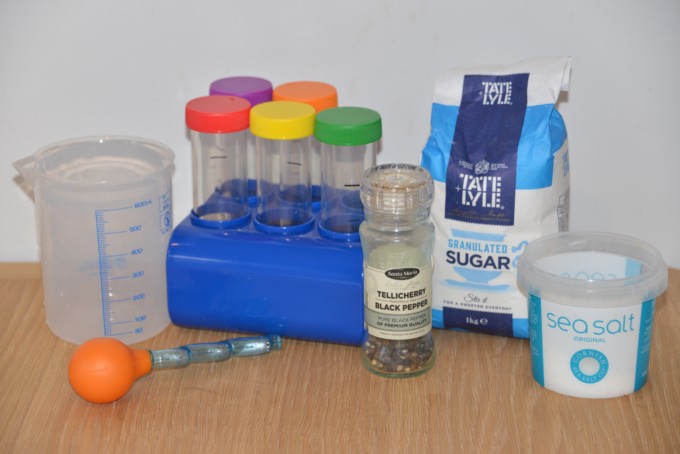
You’ll need
- Transparent containers – test tubes or beakers
- Water ( warm and cold )
- Substances to try to dissolve, e.g. sugar, coffee, pepper, sand, flour, salt.
Instructions
Add a teaspoon of whichever solid you are testing to a glass of cold water and a glass of warm water. Stir and observe the difference.
Watch to see if the solid dissolves in warm and cold water and if one is better than the other.
Remember to use the same amount of each solid and the same amount of cold and warm water to make the investigation a fair test.
Can you design a chart for recording your observations?
Which solids dissolve in water
Things like salt, sugar and coffee dissolve in water. They are soluble. They usually dissolve faster and better in warm or hot water.
Pepper and sand are insoluble; they will not dissolve even in hot water.
Dissolving for older children
Everything is made of particles which are constantly moving. When a soluble solid ( solute ) is mixed with a suitable liquid (solvent), it forms a solution. This process is called dissolving.
Two things that affect the speed at which a solid dissolves are temperature and the size of the grains of the solid.
Caster sugar, made of fine particles, will dissolve quickly, but bigger sugar particles will take longer.
Solids dissolve faster in hot water; in hot water, molecules move more quickly, so they bump into each other more often, increasing the rate of reaction.
An example of a physical change
Dissolving is an example of a physical change. The particles involved are rearranged, but no chemical bonds are changed.
In a physical change, there is no change in mass. If you dissolved 10g of salt in 100g of water, you’d have 110g of solution.
More Dissolving Experiments
Make a naked egg and watch as vinegar dissolves the calcium carbonate of the eggshell.
Lava lamps work because the effervescent tablet dissolves in water releasing carbon dioxide.
Handy definitions
Solute – the solid being dissolved
Solvent – the liquid the solid is dissolving into.
Solution – the solute and the solvent
Soluble – solute that does dissolve
Solubility – how much of a solute will dissolve
Insoluble – does not dissolve
Saturated – a solution that won’t dissolve any more solute at that temperature.
More Science for Kids
Don’t forget we have lots more easy science experiments for kids at home that you can try too!
You might also like our science books! This IS Rocket Science contains 70 fun space experiments for kids, including bottle rockets, film canister rockets, space marble runs and shadow puppets.
Snackable Science contains 60 tasty and edible science snacks!!
Contains affiliate links
Last Updated on April 9, 2024 by Emma Vanstone




For some reason, I struggled to understand solids dissolving in liquids. It was probably until I was in high school and taking Chemistry before I really got it. 😉 I like the little experiment.
Glad you like it, we aim to please. xx
what simple experiments, my little one will be fascinated by this.
Thanks, My 4 year old loved trying all the different things! x
I just needed to get this information for my butterfly garden but after Reading this i will try to do this when i have a science project
Very fun & simple enough for my little ones! Welcome to TGIF LInky Party. Thanks for linking up. Don’t forget to grab the TGIF button for your post or sidebar so others can find the party & link up too. Thanks & see you next week,
Beth =-)
Thanks Beth. x
You do really come up with fabulous experiments to do at home 🙂
Thank you for joining Kids Get Crafty!
Maggy
Thanks Maggy, glad you liked it. x
I am fascinated by this & want to try it! Thanks for linking your idea to the Sunday Showcase last week. Hope to see you this week!
Bern
http://momto2poshlildivas.blogspot.com/search/label/Sunday%20Showcase
Yay, so glad you like it, let us know how you get on. x
simple but effective
Had so much fun doing this for homework, you basically saved me in a desperate situation, simple but very effective ;0)
do all solids dissolve in water?
not all of them
what other solids dissolve?
Loved this experiment – My daughter is nearly 5 and she loved setting up and carrying out the experiment 🙂 We wrote about it first a nd then after we wrote our findings down and then the sciency part too – She has to practise her sentence writing for school (she is in YR R) and it’s not a secret that my daughter loves to write. I wanted to give her a reason to write so experiments are a great way so I don’t have to pluck a random sentence out of the air on demand – THANK YOU THANK YOU THANK YOU!
So cool!
most coolest thing i have ever seen
Yeet
Yeet
Was a very fun experiment and also very fun to do…
Had a fun learning experience with the simple ,little experiment… during theory classes I wasn’t able to understand until I got to do this experiment..the for coming up with the idea.
Wish u luck for upcoming experiments. Love .MELLOW